How Bike Calculator works
The three major forces that must be overcome to maintain a certain speed are air resistance, rolling resistance, and gravity. There is also some frictional force in the chain, gears, and bearings.
The sum of those forces can be multiplied by speed - this is the quantity known as "power". In metric units, we're talking about newtons (a unit of force) times meters/second. It's more common in engineering to use a unit of power that comes from electrical units - watts. In the U.S., we all know that horsepower is a unit of power. One HP is 746 watts.
The only force in cycling that is easy to figure out is gravity, but I mean only the force you must resist as you climb, or the force that pushes you along when you descend. It turns out that the "grade" of a road - the rise divided by the distance traveled - is a quantity you can multiply by your weight to get the force of gravity. For example, if you and your bike weigh 200 lbs and you are riding up a 1% grade, there is 2 lbs of gravity force holding you back. An inconvenient thing about "weight" is that kg is a unit of mass, not a unit of force, so it must be converted to newtons. Measuring grade with a ruler and a level is not such an easy thing, but the combination of a reasonably long distance and a topological map will provide a decent value. A good barometric altimeter can work well, too. GPS readings for elevation are highly inaccurate, however - the satellites are rarely in a good position.
Rolling resistance is figured by multiplying weight by a number that gives the force, the coefficient of rolling resistance. Everyone knows there is more resistance from a knobby mountain bike tire than a 23mm road bike tire - the MTB tire has a higher coefficient of rolling resistance. While this seems simple, there is a problem: it is difficult to make the measurements required to arrive at these coefficients. There are big tables of coefficients you can find on the internet, yes, but those measurements are from tests conducted on steel drums. Real world rolling resistance will be different, mostly because the actual road surface has a big effect.
Aerodynamics is a fundamentally complex and difficult subject. However, there is a simple computational approach for computing resistance by multiplying air velocity squared by some values. Air velocity is the sum of your speed over the ground and the speed of the wind if coming from directly ahead (subtract if coming directly from behind). One of the other values is air density, which depends on temperature and pressure. Pressure depends mostly on elevation. Another value depends on your shape - this is the "Cd" you may have seen elsewhere. A flat plate has a Cd of 1.00 while a very aerodynamic car might be around 0.30. The final value is your frontal area, which varies with your position on the bike.
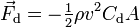
As you may perceive, it is very difficult to calculate an accurate aerodynamic resistance, the largest force a performance-oriented cyclist feels most of the time. Rolling resistance measurements are also troublesome. Good grade measurements are rare, too.
Given the limits in estimating the resisting forces accurately, you might think that it's pointless to try to calculate the relationship between power and speed. Take heart! There is a wonderful adage that applies: "All engineering models are wrong, but some are useful." Check out the Examples page.
Back to the details: Once you know the three forces you need to resist, you can easily compute the power required to maintain a certain speed. Power is force multiplied by speed - pretty simple.
If you want to calculate speed from power, however, you run into the general difficulty of solving a non-linear equation. As I noted above, air resistance depends on the square of speed. Power is this resistance times speed, so overall, the power required to overcome air resistance is related to the third power of speed - a cubic relationship. The full expression involves a squared term (quadratic) as well, due to the head wind component. Solving a cubic equation "backwards" as you must do to figure speed from power is not straightforward. Bike Calculator uses Newton's Method - a fancy trial-and-error method that does the easier "frontwards" calculation typically about eight times before reaching the displayed precision.
I've omitted a detail: if you apply 200 watts to the pedals, how many make it to the pavement? There's friction in the bearings, chain, sprockets, derailleuer, and even in the shoe-to-pedal interface. How much? I don't think anyone knows! Bike Calculator uses a guess of 5%. You can make your own guess in the older calculators.
Note that Bike Calculator could be used for a motor vehicle in exactly the same way - I've used the numeric version to do some calculations for my Prius. On a bike, you are the motor, otherwise everything else is mechanically the same. It is not a physiological model. Sometimes people write me wondering why it shows they'll go faster in hot weather when in their experience they go slower. If their "motor" manages to put out the same power, the higher temperature means lower air density and lower air resistance. Bike Calculator does not consider the effect of the weather on the motor.
Bike Calculator does touch upon a couple of physiological phenomena in the ancillary results: the calories or kilojoules consumed, and weight loss. The energy consumption estimate involves an efficiency factor, basically in the conversion of glucose to muscular output. As you might imagine, this is somewhat variable, even within an individual. Bike Calculator uses 25%, the upper end of the range - a highly-trained, major muscle group ought to be among the most efficient. There are more complications, of course: if you are converting fat to glucose on a ride, there is some loss of efficiency. There is also the complication of whether the food you eat after a ride is replacing lost glucose or being converted to fat. If you find yourself wondering exactly what a food calorie represents, you're beginning to understand.
The calorie or kilojoule figure that Bike Calculator computes is from the energy you put out on the bike divided by the efficiency factor. Basal metabolism is not included. Stationary bikes that display energy expenditure may include metabolism and a different efficiency assumption. They may use an actual power measurement (e.g., a high-end LifeCycle), but it is more likely that they just make something up at the direction of their marketing department.
Weight loss is the caloric consumption divided by food energy content of fat. In the U.S., serious dieters know this is 3500 cal/lb. Properly applying this to real-life situations involves a few complications (mainly, the relationship between calorie intake and basal metabolism), but the underlying principle is the First Law of Thermodynamics.

