

1. On your first ride in the spring, you fall 43 seconds behind your personal best, which you set the previous August in hot weather. You wonder how much of that 43 seconds is from the increased air resistance from colder, denser air. You enter all the correct parameters for the August ride, and adjust power to give the actual time. This power seems a little low, but the loop was a little hilly, so you add a little grade and adjust power again. Then you change the temperature and find that the time increases by 54 seconds. So, it appears your winter training was good.
2. You'd like to do the Whiteface Mountain Climb. You've looked up the finish times of past participants, and you'd like to know how you'll compare. There's two sections with different grades, so you enter all your parameters and do the calculation for each segment and add the times to get a total. Looks like you're not going to do too well, and worse, your predicted speed means you'll be standing most of the way. So, you start dieting and check Ebay for a different cassette.
3. What? The Tour de France guys are going 20 kph up an 8% grade? How many watts is that, and how fast would you go? OMG.
4. You're at risk of missing your weight goal this month. You need to lose 5 lbs this week! That's 17,500 calories you've got to burn without replacing. You're willing to eat 500 calories less than your basal metabolism per day, that's 3500 calories, leaving 14,000 to go - 2000 per day. What kind of ride is that? (About 60 miles - oops!)
5. Gosh, those new bikes are pretty - and light! You hate getting dropped by that new guy on the Los Alamos road - let's see, he crests the hill about 30 seconds in front of you, so ... ah! 1500 grams will buy you 33 seconds on that hill! The black model with the red fade may be even faster.
6. You wonder what the grade is on that hill on Igerna Road. Map my Ride says 4% but that can't be right. You're usually hitting about 33 mph when coasting down (power = 0), so ... it must be about 6.3%.
Have you ever wondered how much faster you would go if you spent $5 on a pair of titanium water bottle cage screws? How much faster you would go if you lost ten pounds? Whether you should go anaerobic up that short hill? If that almost imperceptible headwind could be responsible for your slow speed (and not last night's chili)?
Let's answer some simple questions. First, why are even small headwinds so unpleasant? The following graph shows the effect on a rider putting out 150 watts for two positions, on the hoods (lower) and using an aerobar (upper):
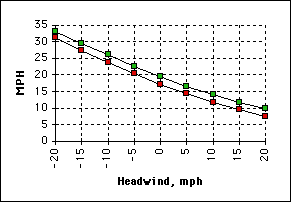
A headwind of 5 mph reduces speed by nearly 3 mph. This is the equivalent of a 0.73% grade. You would have to increase power from 150 to 215 watts to compensate (see one of the "Power" calculators). And don't we all try, slaves to our cyclocomputers?
Here is the effect of grade on speed, for the same two positions (hoods and aerobar), at 150 watts:
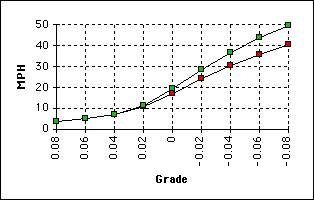
How does weight influence these curves? If you lost 10 lbs (about 5%), you would be able to go about 5% faster on the steepest hills and 0.4% faster on the level; you'd go about 2% slower on the downhills.
Over a simulated 20-mile closed-circuit ride with a variety of grades, a 10-lb difference produced a 33 second difference. (You can do this sort of calculation with one of the "Six Segment" calculators in the "Old Stuff" section.) This may or may not seem significant in the context of a time trial. On the other hand, there were two hills on this simulated route where the heavier rider falls back 14 seconds. That is, about 200 feet back and well-dropped. A two-lb difference that you can buy at a bike shop for $500 amounts to only 7 seconds on this circuit, but again, a two-lb penalty can mean cresting a hill 50 feet behind your better-sponsored buddies.
Here is a chart that gives speed versus power for the same two positions again:
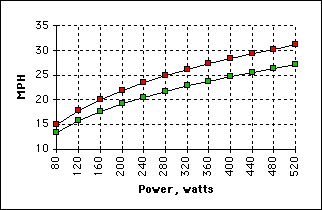
The advantage of the aero position seems overstated (it is more accepted that it is worth one or two mph). But for many, the aerobar position is not entirely comfortable, and they cannot peddle as hard. (Losing ten pounds might provide an added bonus here.)
If you can do 17.2 mph when riding on the brake hoods on a road bike with thin high pressure tires, you can only expect to go 14.4 mph on a fat tire mountain bike. This results from the increase in rolling resistance from 0.004 to 0.012. (Trivia: it is the low pressure of fat tires that increases rolling resistance.)
What do the pro's put out? In the final stage of the 1989 Tour de France, Greg Lemond averaged 34 mph with a 5 mph tailwind. According to the sort of calculations you can do here, he was putting out 513 watts. Possible? Perhaps the tailwind was stronger.